Transformasi Laplace dalam Dunia Kendali & Telekomunikasi: Mengubah Persamaan Jadi Solusi

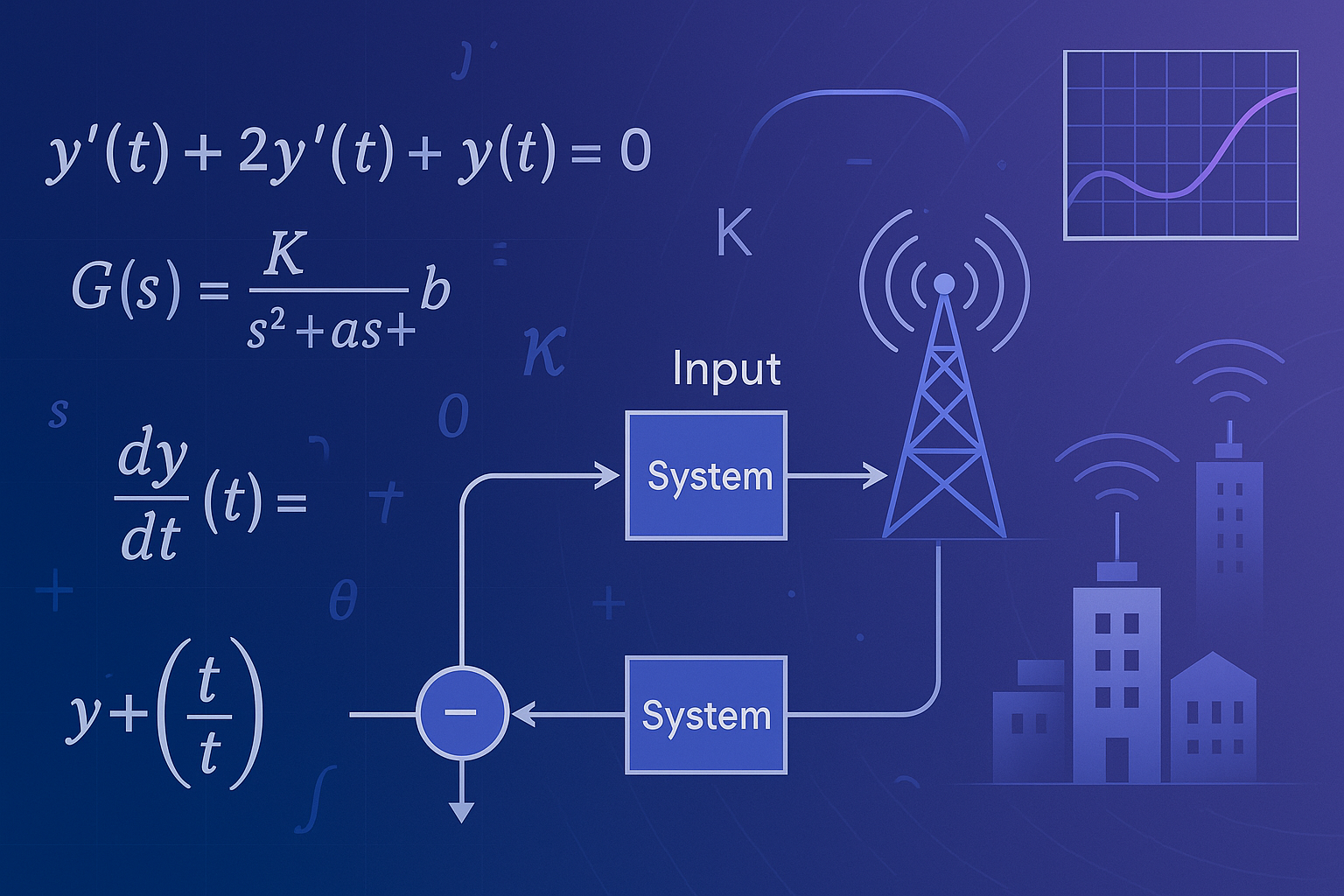
Di ruang kelas teknik, papan tulis sering penuh dengan persamaan diferensial yang tampak “menakutkan”. Di dunia industri, persamaan yang sama menentukan apakah robot bergerak stabil, antena mengarah dengan tepat, atau sinyal komunikasi tetap jernih di tengah gangguan. Transformasi Laplace adalah jembatan yang menghubungkan keduanya. Ia mengubah persamaan menjadi alat desain yang bisa langsung dipakai insinyur untuk memecahkan masalah nyata.

Berbagai studi menunjukkan bahwa Transformasi Laplace menjadi tulang punggung analisis sistem di banyak cabang rekayasa, mulai dari rangkaian listrik, sistem kendali, hingga teknik komunikasi dan pemrosesan sinyal.

Secara konsep, Transformasi Laplace mengubah fungsi waktu menjadi fungsi di domain kompleks dengan variabel s. Di domain ini, operasi turunan dan integral berubah menjadi operasi aljabar yang jauh lebih mudah ditangani.

Beberapa manfaat kunci Transformasi Laplace yang disorot dalam berbagai tinjauan literatur:

• Menyederhanakan persamaan diferensial linier menjadi persamaan aljabar.
• Memudahkan analisis sistem linier waktu invarian melalui fungsi alih.
• Mendukung analisis respon transien dan mantap, termasuk nilai awal dan nilai akhir.IJRITCC+1

Hasil kajian literatur terbaru juga menegaskan bahwa Laplace tetap relevan dalam perancangan sistem teknik modern, bukan hanya sebagai teori kuliah, tetapi sebagai alat kerja untuk merancang sistem yang efisien dan stabil.

Dalam sistem kendali, perilaku dinamik sering dimodelkan sebagai persamaan diferensial. Transformasi Laplace digunakan untuk:

1. Mengubah persamaan diferensial menjadi persamaan aljabar.
2. Mendefinisikan fungsi alih G(s) sebagai perbandingan antara Laplace keluaran dan masukan.
3. Menganalisis stabilitas dan performa, terutama di sistem umpan balik.

Penelitian tentang fungsi alih dan stabilitas menunjukkan bahwa pemodelan di domain s memudahkan analisis sistem tertutup, termasuk sistem dengan keterlambatan waktu dan parameter yang berubah terhadap waktu.cims.fti.dp.ua+1

Pendekatan ini digunakan, misalnya, untuk:

• Menentukan posisi kutub dan nol.
• Menganalisis respon sistem terhadap masukan langkah, ramp, atau sinus.
• Mendesain pengendali seperti PID agar overshoot, waktu naik, dan error keadaan mapan berada dalam spesifikasi.

Di dunia telekomunikasi, sinyal melewati banyak blok sistem seperti rangkaian filter, penguat, kanal transmisi, dan rangkaian penyesuai impedansi. Blok blok ini biasanya dimodelkan sebagai sistem linier waktu invarian yang bisa dijelaskan dengan fungsi alih di domain Laplace.

Beberapa perannya antara lain:

• Merancang filter analog dengan menentukan fungsi alih yang diinginkan, lalu menerjemahkannya menjadi rangkaian RLC.
• Menganalisis respon frekuensi kanal komunikasi melalui hubungan antara fungsi alih dan karakteristik amplitudo fase.
• Menghubungkan analisis di domain s dengan transformasi Fourier untuk melihat spektrum sinyal.Wikibooks+1

Sejumlah penelitian juga mengembangkan transformasi Laplace dua dimensi sebagai alat analisis sistem komunikasi yang melibatkan variasi ganda, misalnya waktu dan ruang atau waktu dan frekuensi, untuk memodelkan kanal dan sistem yang lebih kompleks.

Contoh Kasus : Kendali Posisi Antena pada Sistem Komunikasi

Bayangkan sebuah antena parabola yang harus selalu mengarah tepat ke satelit. Jika sudut antena meleset sedikit saja, kualitas sinyal menurun. Sistem mekanik antena bisa dimodelkan sebagai sistem orde dua:$$J \,\theta”(t) + b \,\theta'(t) + k \,\theta(t) = K \,u(t)$$Jθ′′(t)+bθ′(t)+kθ(t)=Ku(t)

dengan

• θ(t) sudut antena
• u(t) sinyal kendali dari motor
• J momen inersia
• b koefisien redaman
• k konstanta kekakuan
• K penguatan aktuator

Langkah pengguna Transformasi Laplace:

1. Ambil Transformasi Laplace dari kedua sisi persamaan (diasumsikan kondisi awal nol), sehingga turunan terhadap waktu berubah menjadi perkalian dengan s di domain Laplace.
2. Susun rasio Θ(s) terhadap U(s) untuk mendapatkan fungsi alih G(s) di domain s, yang berbentuk:

$$G(s) = \frac{\Theta(s)}{U(s)} = \frac{K}{J s^{2} + b s + k}$$

3. Dari G(s), insinyur dapat:
   • Menghitung respon terhadap masukan langkah (perubahan set sudut tiba tiba).
   • Menganalisis posisi kutub untuk melihat apakah sistem stabil dan seberapa cepat antena mencapai sudut yang diinginkan.
   • Mendesain pengendali PD atau PID di domain s, lalu mengatur parameter pengendali agar overshoot kecil, waktu tunak cepat, dan error keadaan mapan kecil.

Dalam penelitian tentang sistem kendali orde pecahan dan sistem dengan parameter yang tidak integer, Transformasi Laplace juga digunakan untuk mendapatkan fungsi alih yang mengandung pangkat s pecahan. Hal ini menunjukkan fleksibilitas Laplace dalam menangani model sistem yang lebih realistis.

Contoh Kasus : Filter Analog pada Penerima Telekomunikasi

Di sisi penerima suatu sistem komunikasi, sinyal yang diterima biasanya tercampur dengan noise frekuensi tinggi. Sebuah filter analog jenis low pass dapat dipakai untuk meredam komponen frekuensi tinggi agar sinyal informasi utama tetap jernih.

Misalnya, sebuah rangkaian RC sederhana dengan:$$R \,\frac{dy(t)}{dt} \,C + y(t) = x(t)$$Rdtdy(t)​C+y(t)=x(t)

dengan x(t) sinyal masukan dan y(t) sinyal keluaran.

Langkah analisis dengan Transformasi Laplace:

1. Transformasi persamaan di atas ke domain s sehingga turunan berubah menjadi s dikalikan Laplace y(t).
2. Susun rasio Y(s) terhadap X(s) untuk mendapatkan fungsi alih H(s):

$$H(s) = \frac{Y(s)}{X(s)} = \frac{1}{R C s + 1}$$

3. Dari H(s), diperoleh:
   • Frekuensi potong, yang biasanya berkaitan dengan 1 dibagi 2πRC.
   • Respon langkah yang menggambarkan seberapa cepat filter merespon perubahan sinyal.
   • Bentuk respon frekuensi yang menunjukkan seberapa besar peredaman terhadap noise di frekuensi lebih tinggi.

Pendekatan seperti ini sesuai dengan paparan berbagai makalah yang meninjau peran Transformasi Laplace dalam analisis rangkaian listrik dan sistem komunikasi, untuk merancang filter dan kanal yang memenuhi spesifikasi tertentu.

Transformasi Laplace bukan sekadar bab di mata kuliah matematika teknik. Ia adalah “bahasa kerja” yang memudahkan insinyur sistem kendali dan telekomunikasi mengubah persamaan menjadi solusi nyata.

Di sistem kendali, Laplace mengubah model diferensial menjadi fungsi alih yang bisa dianalisis dan dirancang secara sistematis. Di telekomunikasi, Laplace membantu memodelkan filter, kanal, dan blok sistem lain dalam bentuk yang mudah ditautkan dengan spesifikasi frekuensi dan kualitas layanan.

Perkembangan terbaru juga menunjukkan munculnya transformasi turunan Laplace dan transformasi sejenis yang memperluas kemampuan analisis untuk sistem yang lebih kompleks, tetapi ide dasarnya tetap sama: bawa persoalan ke domain yang lebih mudah, selesaikan di sana, lalu kembali ke dunia nyata sebagai solusi yang bisa diimplementasikan.

Referensi Jurnal dan Sumber Ilmiah

1. Patil et al., “A Literature Review on Applications of Laplace Transform in Engineering”. ResearchGate
2. Ibrahim S., “Application of Laplace Transform in Science and Engineering”, International Journal of Research in IT and Communication. IJRITCC
3. IRJET, “Applications of Laplace Transform in Science and Engineering Fields”. IRJET
4. Avdieiev V., “Transfer functions of a time-varying control system”. cims.fti.dp.ua
5. “Two-dimensional Laplace transform based analysis for communication systems”. ResearchGate